Part 2 Mixed effects models
A mixed model, also known as a hierarchical or multilevel model, in general contains both random (subject or group level) and fixed (population level) effects.
2.1 Restricted maximum likelihood
The standard way for fitting mixed effects models in R is lme4 (Bates et al. 2020), which estimates the parameters via restricted maximum likelihood optimization.
A canonical example dataset is sleepstudy, bundled with the package, which records reaction times each day for 18 subjects restricted to three hours of sleep per night.
The data are visualised in Figure 2.1.
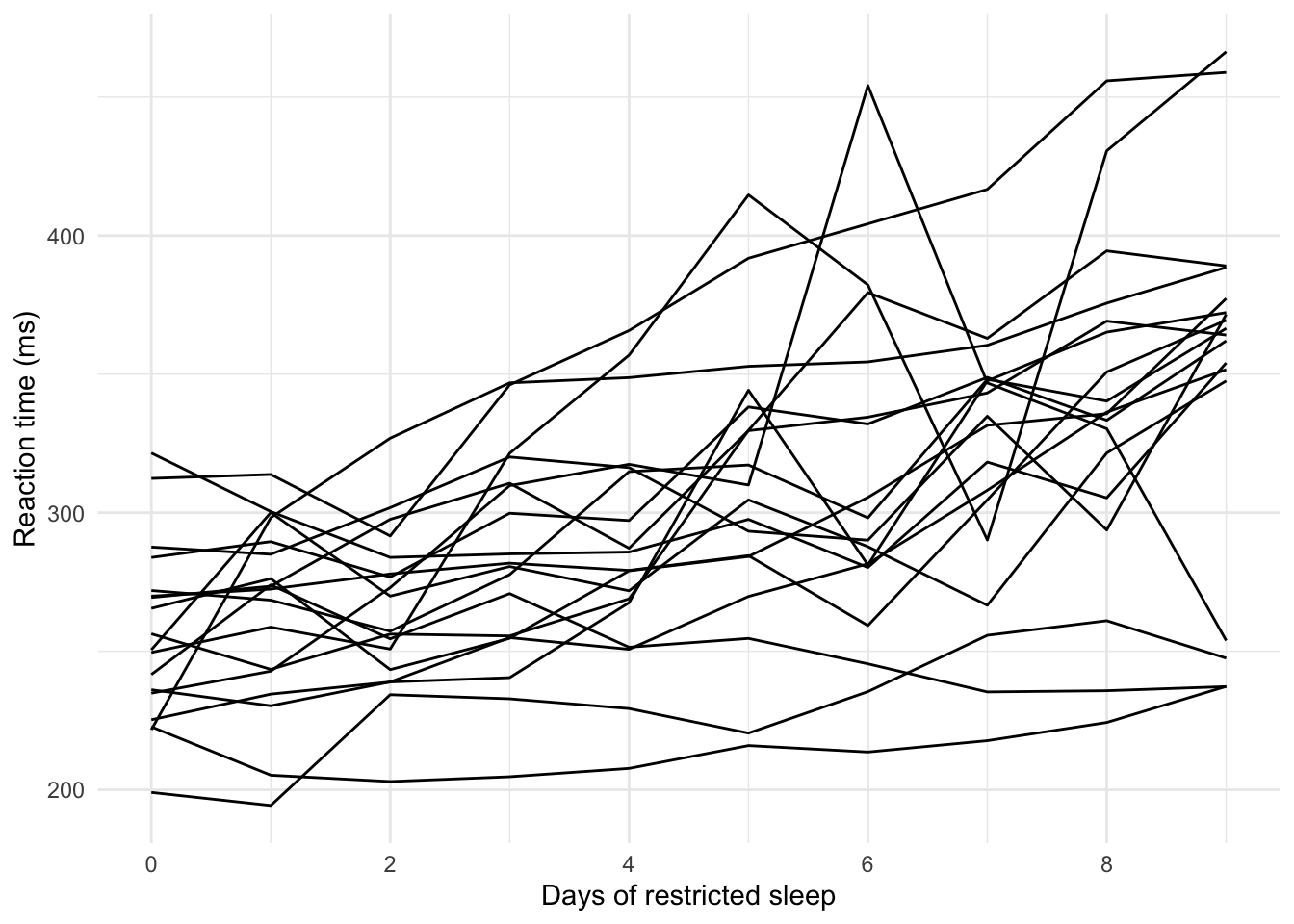
Figure 2.1: Average reaction time per day (ms) for 18 subjects in a sleep deprivation study. Each line represents one subject
Overall, we would probably expect reaction times to increase as the subjects become more sleep-deprived. But some subjects surely will have had faster reaction times than others, even before the study began. This is modelled using a random intercept coefficient. Meanwhile, we might assume each day of sleep deprivation results in the same increase in reaction time for every participant, in which case a common, fixed slope coefficient is appropriate. However, if instead we thought the daily effect of sleep deprivation varied between subjects, we could fit random slopes (as well as the random intercept).
In lme4 syntax, the random intercept model is
which yields the following summary output.
Linear mixed model fit by REML ['lmerMod']
Formula: Reaction ~ Days + (1 | Subject)
Data: sleepstudy
REML criterion at convergence: 1786.5
Scaled residuals:
Min 1Q Median 3Q Max
-3.2257 -0.5529 0.0109 0.5188 4.2506
Random effects:
Groups Name Variance Std.Dev.
Subject (Intercept) 1378.2 37.12
Residual 960.5 30.99
Number of obs: 180, groups: Subject, 18
Fixed effects:
Estimate Std. Error t value
(Intercept) 251.4051 9.7467 25.79
Days 10.4673 0.8042 13.02
Correlation of Fixed Effects:
(Intr)
Days -0.371Adding a random slope, we obtain
Linear mixed model fit by REML ['lmerMod']
Formula: Reaction ~ Days + (Days | Subject)
Data: sleepstudy
REML criterion at convergence: 1743.6
Scaled residuals:
Min 1Q Median 3Q Max
-3.9536 -0.4634 0.0231 0.4634 5.1793
Random effects:
Groups Name Variance Std.Dev. Corr
Subject (Intercept) 612.10 24.741
Days 35.07 5.922 0.07
Residual 654.94 25.592
Number of obs: 180, groups: Subject, 18
Fixed effects:
Estimate Std. Error t value
(Intercept) 251.405 6.825 36.838
Days 10.467 1.546 6.771
Correlation of Fixed Effects:
(Intr)
Days -0.138The correlation between the random effects is close to zero.
2.2 Markov chain Monte Carlo
Researchers who prefer a Bayesian approach can take advantage of the rstanarm (Gabry and Goodrich 2020) and brms (Bürkner 2020) packages, which allow specifying analogous Bayesian models, fitted using Hamiltonian Monte Carlo (rather than restricted maximum likelihood) but using the familiar lme4-style formula syntax.
If using default priors, the code is nearly identical.
The package rstanarm (applied regression modelling via RStan) has a series of functions with the prefix stan_ that are analogous to common frequentist methods, e.g. stan_glm and, in this case, stan_lmer:
stan_lmer
family: gaussian [identity]
formula: Reaction ~ Days + (Days | Subject)
observations: 180
------
Median MAD_SD
(Intercept) 251.3 6.6
Days 10.4 1.7
Auxiliary parameter(s):
Median MAD_SD
sigma 25.9 1.6
Error terms:
Groups Name Std.Dev. Corr
Subject (Intercept) 24.3
Days 6.9 0.08
Residual 26.0
Num. levels: Subject 18
------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanregMeanwhile, brms (Bayesian regression modelling with Stan), which is designed for fitting Bayesian multilevel models, has a single workhorse function, brm, which also uses lme4-style formulae:
Family: gaussian
Links: mu = identity; sigma = identity
Formula: Reaction ~ Days + (Days | Subject)
Data: sleepstudy (Number of observations: 180)
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup samples = 4000
Group-Level Effects:
~Subject (Number of levels: 18)
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept) 26.89 6.90 15.67 42.53 1.00 1637 1891
sd(Days) 6.56 1.51 4.13 9.95 1.00 1383 2191
cor(Intercept,Days) 0.09 0.31 -0.47 0.71 1.00 872 1352
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept 251.32 7.47 236.12 265.87 1.00 1578 1641
Days 10.38 1.68 7.00 13.70 1.00 1599 2094
Family Specific Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 25.94 1.56 23.05 29.14 1.00 3318 2783
Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).As with other Stan wrapper packages, if you don’t specify any prior distributions, then uninformative ones will be used by default. This is usually fine in this case but you’ll need to set explicit priors when fitting more complicated models.
All three of lme4, rstanarm and brms yield similar parameter estimates for the sleep deprivation study model with random intercepts and slopes:
- fixed intercept about 251 ms
- fixed slope about 10.5 ms per day
- random intercept standard deviation about 24 ms
- random slope standard deviation about 6 ms per day
- random intercept–slope correlation about 0.07–0.08
At this juncture, it’s worth pointing out that the package lcmm (Proust-Lima, Philipps, and Liquet 2017) can be used to compute a model equivalent to lme4 when the number of latent classes is specified to be equal to one.
The function hlme (or lcmm with link = 'linear') has a slightly different way of specifying the formulae: random effects and levels of the model are specified separately from the fixed effects via the random and subject arguments, rather than the lme4-style (var | group) syntax.
For some reason, the variable passed to subject also has to be numeric, rather than a factor.
library(lcmm)
lcm_slope <- hlme(fixed = Reaction ~ Days,
random = ~ Days,
subject = 'Subject',
ng = 1,
data = transform(sleepstudy, Subject = as.numeric(Subject)))Heterogenous linear mixed model
fitted by maximum likelihood method
hlme(fixed = Reaction ~ Days, random = ~Days, subject = "Subject",
ng = 1, data = transform(sleepstudy, Subject = as.numeric(Subject)))
Statistical Model:
Dataset: transform(sleepstudy, Subject = as.numeric(Subject))
Number of subjects: 18
Number of observations: 180
Number of latent classes: 1
Number of parameters: 6
Iteration process:
Convergence criteria satisfied
Number of iterations: 17
Convergence criteria: parameters= 9.7e-07
: likelihood= 1.6e-08
: second derivatives= 2.5e-15
Goodness-of-fit statistics:
maximum log-likelihood: -875.97
AIC: 1763.94
BIC: 1769.28
Maximum Likelihood Estimates:
Fixed effects in the longitudinal model:
coef Se Wald p-value
intercept 251.40511 6.63228 37.906 0.00000
Days 10.46729 1.50224 6.968 0.00000
Variance-covariance matrix of the random-effects:
intercept Days
intercept 565.51538
Days 11.05543 32.6822
coef Se
Residual standard error: 25.59182 1.50838The summary output includes a variance-covariance matrix for the random effects, rather than giving correlations. It’s easy enough to calculate one from the other and verify the random correlation estimate is equivalent to the other packages:
coef Se Wald test p_value
Var(intercept) 565.51538 265.29710
Cov(intercept,Days) 11.05543 42.85392 0.25798 0.79642
Var(Days) 32.68220 13.57460 Cov(intercept,Days)
0.08132008 However if you aren’t planning on fitting a mixture model then the other packages probably have more concise syntax.
References
Bates, Douglas, Martin Maechler, Ben Bolker, and Steven Walker. 2020. Lme4: Linear Mixed-Effects Models Using Eigen and S4. https://github.com/lme4/lme4/.
Bürkner, Paul-Christian. 2020. Brms: Bayesian Regression Models Using Stan. https://CRAN.R-project.org/package=brms.
Gabry, Jonah, and Ben Goodrich. 2020. Rstanarm: Bayesian Applied Regression Modeling via Stan. https://CRAN.R-project.org/package=rstanarm.
Proust-Lima, Cécile, Viviane Philipps, and Benoit Liquet. 2017. “Estimation of Extended Mixed Models Using Latent Classes and Latent Processes: The R Package lcmm.” Journal of Statistical Software 78 (2): 1–56. https://doi.org/10.18637/jss.v078.i02.